跳转至

1266. 访问所有点的最小时间

题目描述

平面上有 n 个点，点的位置用整数坐标表示 points[i] = [xi, yi] 。请你计算访问所有这些点需要的 最小时间（以秒为单位）。

你需要按照下面的规则在平面上移动：

  • 每一秒内，你可以：
    • 沿水平方向移动一个单位长度，或者
    • 沿竖直方向移动一个单位长度，或者
    • 跨过对角线移动 sqrt(2) 个单位长度（可以看作在一秒内向水平和竖直方向各移动一个单位长度）。
  • 必须按照数组中出现的顺序来访问这些点。
  • 在访问某个点时，可以经过该点后面出现的点，但经过的那些点不算作有效访问。

 

示例 1：

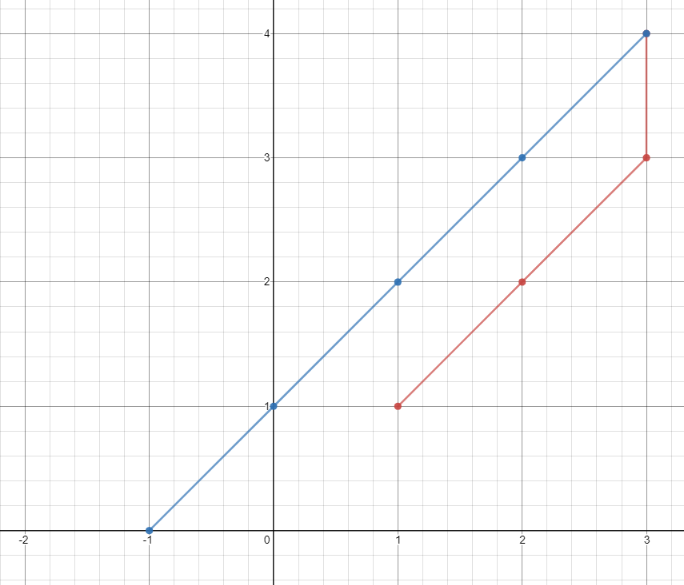
输入：points = [[1,1],[3,4],[-1,0]]
输出：7
解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
从 [1,1] 到 [3,4] 需要 3 秒 
从 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒

示例 2：

输入：points = [[3,2],[-2,2]]
输出：5

 

提示：

  • points.length == n
  • 1 <= n <= 100
  • points[i].length == 2
  • -1000 <= points[i][0], points[i][1] <= 1000

解法

方法一：模拟

对于两个点 $p1=(x_1, y_1)$ 和 $p2=(x_2, y_2)$，横坐标和纵坐标分别移动的距离分别为 $dx = |x_1 - x_2|$ 和 $dy = |y_1 - y_2|$。

如果 $dx \ge dy$，则沿对角线移动 $dy$，再沿水平方向移动 $dx - dy$；如果 $dx < dy$，则沿对角线移动 $dx$，再沿竖直方向移动 $dy - dx$。因此，两个点之间的最短距离为 $max(dx, dy)$。

我们可以遍历所有的点对，计算出每个点对之间的最短距离，然后求和即可。

时间复杂度 $O(n)$，其中 $n$ 为点的个数。空间复杂度 $O(1)$。

1
2
3
4
5
class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        return sum(
            max(abs(p1[0] - p2[0]), abs(p1[1] - p2[1])) for p1, p2 in pairwise(points)
        )

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution {
    public int minTimeToVisitAllPoints(int[][] points) {
        int ans = 0;
        for (int i = 1; i < points.length; ++i) {
            int dx = Math.abs(points[i][0] - points[i - 1][0]);
            int dy = Math.abs(points[i][1] - points[i - 1][1]);
            ans += Math.max(dx, dy);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int ans = 0;
        for (int i = 1; i < points.size(); ++i) {
            int dx = abs(points[i][0] - points[i - 1][0]);
            int dy = abs(points[i][1] - points[i - 1][1]);
            ans += max(dx, dy);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func minTimeToVisitAllPoints(points [][]int) (ans int) {
    for i, p := range points[1:] {
        dx := abs(p[0] - points[i][0])
        dy := abs(p[1] - points[i][1])
        ans += max(dx, dy)
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

1
2
3
4
5
6
7
8
9
function minTimeToVisitAllPoints(points: number[][]): number {
    let ans = 0;
    for (let i = 1; i < points.length; i++) {
        let dx = Math.abs(points[i][0] - points[i - 1][0]),
            dy = Math.abs(points[i][1] - points[i - 1][1]);
        ans += Math.max(dx, dy);
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
impl Solution {
    pub fn min_time_to_visit_all_points(points: Vec<Vec<i32>>) -> i32 {
        let n = points.len();
        let mut ans = 0;
        for i in 1..n {
            let x = (points[i - 1][0] - points[i][0]).abs();
            let y = (points[i - 1][1] - points[i][1]).abs();
            ans += x.max(y);
        }
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
#define max(a, b) (((a) > (b)) ? (a) : (b))

int minTimeToVisitAllPoints(int** points, int pointsSize, int* pointsColSize) {
    int ans = 0;
    for (int i = 1; i < pointsSize; i++) {
        int x = abs(points[i - 1][0] - points[i][0]);
        int y = abs(points[i - 1][1] - points[i][1]);
        ans += max(x, y);
    }
    return ans;
}

评论