


题目描述
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
- 玩家用字符
'S' 表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。
- 地板用字符
'.' 表示,意味着可以自由行走。
- 墙用字符
'#' 表示,意味着障碍物,不能通行。
- 箱子仅有一个,用字符
'B' 表示。相应地,网格上有一个目标位置 'T'。
- 玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
- 玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:
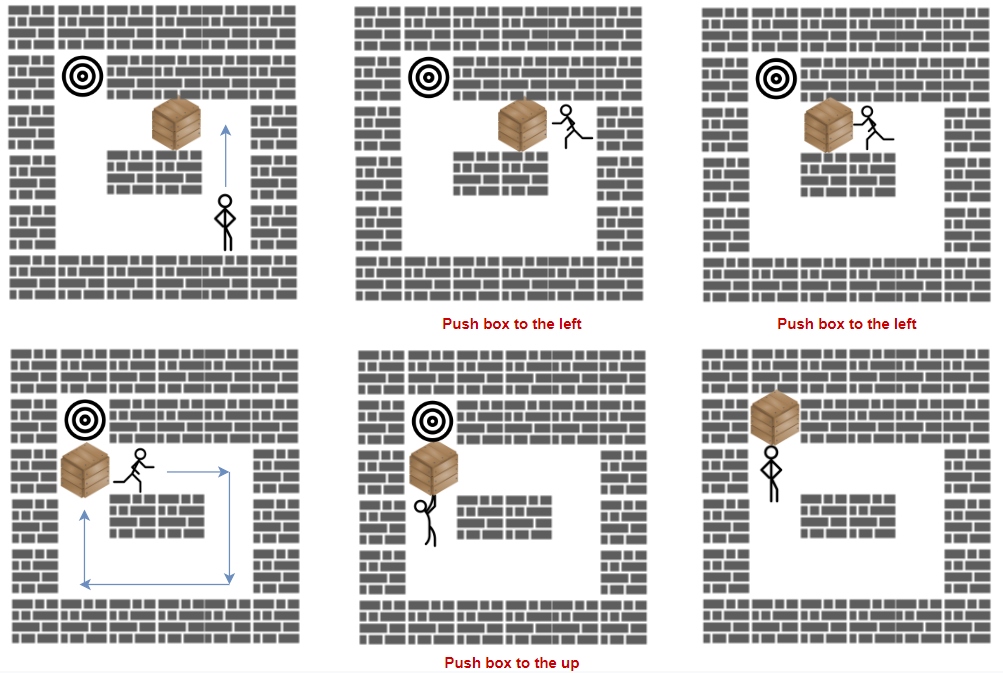
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#",".","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:3
解释:我们只需要返回推箱子的次数。
示例 2:
输入:grid = [["#","#","#","#","#","#"],
["#","T","#","#","#","#"],
["#",".",".","B",".","#"],
["#","#","#","#",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:-1
示例 3:
输入:grid = [["#","#","#","#","#","#"],
["#","T",".",".","#","#"],
["#",".","#","B",".","#"],
["#",".",".",".",".","#"],
["#",".",".",".","S","#"],
["#","#","#","#","#","#"]]
输出:5
解释:向下、向左、向左、向上再向上。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 20grid 仅包含字符 '.', '#', 'S' , 'T', 以及 'B'。grid 中 'S', 'B' 和 'T' 各只能出现一个。
解法
方法一:双端队列 + BFS
我们把玩家的位置和箱子的位置看成一个状态,即 \((s_i, s_j, b_i, b_j)\),其中 \((s_i, s_j)\) 是玩家的位置,而 \((b_i, b_j)\) 是箱子的位置。在代码实现上,我们定义一个函数 \(f(i, j)\),它将二维坐标 \((i, j)\) 映射到一个一维的状态编号,即 \(f(i, j) = i \times n + j\),其中 \(n\) 是网格的列数。那么玩家和箱子的状态就是 \((f(s_i, s_j), f(b_i, b_j))\)。
我们首先遍历网格,找到玩家和箱子的初始位置,记为 \((s_i, s_j)\) 和 \((b_i, b_j)\)。
然后,我们定义一个双端队列 \(q\),其中每个元素都是一个三元组 \((f(s_i, s_j), f(b_i, b_j), d)\),表示玩家位于 \((s_i, s_j)\),箱子位于 \((b_i, b_j)\),并且已经进行了 \(d\) 次推动。初始时,我们将 \((f(s_i, s_j), f(b_i, b_j), 0)\) 加入队列 \(q\)。
另外,我们用一个二维数组 \(vis\) 记录每个状态是否已经访问过,初始时 \(vis[f(s_i, s_j), f(b_i, b_j)]\) 标记为已访问。
接下来,我们开始进行广度优先搜索。
在每一步搜索中,我们取出队头元素 \((f(s_i, s_j), f(b_i, b_j), d)\),并检查是否满足 \(grid[b_i][b_j] = 'T'\),如果是,说明箱子已经被推到目标位置,此时将 \(d\) 作为答案返回即可。
否则,我们枚举玩家的下一步移动方向,玩家新的位置记为 \((s_x, s_y)\),如果 \((s_x, s_y)\) 是一个合法的位置,我们判断此时 \((s_x, s_y)\) 是否与箱子的位置 \((b_i, b_j)\) 相同:
- 如果相同,说明当前玩家到达了箱子的位置,并且推动箱子往前走了一步。箱子新的位置为 \((b_x, b_y)\),如果 \((b_x, b_y)\) 是一个合法的位置,且状态 \((f(s_x, s_y), f(b_x, b_y))\) 没有被访问过,那么我们就将 \((f(s_x, s_y), f(b_x, b_y), d + 1)\) 加入队列 \(q\) 的末尾,并将 \(vis[f(s_x, s_y), f(b_x, b_y)]\) 标记为已访问。
- 如果不同,说明当前玩家没有推动箱子,那么我们只需要判断状态 \((f(s_x, s_y), f(b_i, b_j))\) 是否被访问过,如果没有被访问过,那么我们就将 \((f(s_x, s_y), f(b_i, b_j), d)\) 加入队列 \(q\) 的头部,并将 \(vis[f(s_x, s_y), f(b_i, b_j)]\) 标记为已访问。
继续进行广度优先搜索,直到队列为空为止。
注意,如果推动箱子,那么推动次数 \(d\) 需要加 \(1\),并且新的状态加入到队列 \(q\) 的末尾;如果没推动箱子,那么推动次数 \(d\) 不变,新的状态加入到队列 \(q\) 的头部。
最后,如果没有找到合法的推动方案,那么返回 \(-1\)。
时间复杂度 \(O(m^2 \times n^2)\),空间复杂度 \(O(m^2 \times n^2)\)。其中 \(m\) 和 \(n\) 分别是网格的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution:
def minPushBox(self, grid: List[List[str]]) -> int:
def f(i: int, j: int) -> int:
return i * n + j
def check(i: int, j: int) -> bool:
return 0 <= i < m and 0 <= j < n and grid[i][j] != "#"
for i, row in enumerate(grid):
for j, c in enumerate(row):
if c == "S":
si, sj = i, j
elif c == "B":
bi, bj = i, j
m, n = len(grid), len(grid[0])
dirs = (-1, 0, 1, 0, -1)
q = deque([(f(si, sj), f(bi, bj), 0)])
vis = [[False] * (m * n) for _ in range(m * n)]
vis[f(si, sj)][f(bi, bj)] = True
while q:
s, b, d = q.popleft()
bi, bj = b // n, b % n
if grid[bi][bj] == "T":
return d
si, sj = s // n, s % n
for a, b in pairwise(dirs):
sx, sy = si + a, sj + b
if not check(sx, sy):
continue
if sx == bi and sy == bj:
bx, by = bi + a, bj + b
if not check(bx, by) or vis[f(sx, sy)][f(bx, by)]:
continue
vis[f(sx, sy)][f(bx, by)] = True
q.append((f(sx, sy), f(bx, by), d + 1))
elif not vis[f(sx, sy)][f(bi, bj)]:
vis[f(sx, sy)][f(bi, bj)] = True
q.appendleft((f(sx, sy), f(bi, bj), d))
return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | class Solution {
private int m;
private int n;
private char[][] grid;
public int minPushBox(char[][] grid) {
m = grid.length;
n = grid[0].length;
this.grid = grid;
int si = 0, sj = 0, bi = 0, bj = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'S') {
si = i;
sj = j;
} else if (grid[i][j] == 'B') {
bi = i;
bj = j;
}
}
}
int[] dirs = {-1, 0, 1, 0, -1};
Deque<int[]> q = new ArrayDeque<>();
boolean[][] vis = new boolean[m * n][m * n];
q.offer(new int[] {f(si, sj), f(bi, bj), 0});
vis[f(si, sj)][f(bi, bj)] = true;
while (!q.isEmpty()) {
var p = q.poll();
int d = p[2];
bi = p[1] / n;
bj = p[1] % n;
if (grid[bi][bj] == 'T') {
return d;
}
si = p[0] / n;
sj = p[0] % n;
for (int k = 0; k < 4; ++k) {
int sx = si + dirs[k], sy = sj + dirs[k + 1];
if (!check(sx, sy)) {
continue;
}
if (sx == bi && sy == bj) {
int bx = bi + dirs[k], by = bj + dirs[k + 1];
if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
continue;
}
vis[f(sx, sy)][f(bx, by)] = true;
q.offer(new int[] {f(sx, sy), f(bx, by), d + 1});
} else if (!vis[f(sx, sy)][f(bi, bj)]) {
vis[f(sx, sy)][f(bi, bj)] = true;
q.offerFirst(new int[] {f(sx, sy), f(bi, bj), d});
}
}
}
return -1;
}
private int f(int i, int j) {
return i * n + j;
}
private boolean check(int i, int j) {
return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#';
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 | class Solution {
public:
int minPushBox(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size();
int si, sj, bi, bj;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'S') {
si = i, sj = j;
} else if (grid[i][j] == 'B') {
bi = i, bj = j;
}
}
}
auto f = [&](int i, int j) {
return i * n + j;
};
auto check = [&](int i, int j) {
return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#';
};
int dirs[5] = {-1, 0, 1, 0, -1};
deque<tuple<int, int, int>> q;
q.emplace_back(f(si, sj), f(bi, bj), 0);
bool vis[m * n][m * n];
memset(vis, false, sizeof(vis));
vis[f(si, sj)][f(bi, bj)] = true;
while (!q.empty()) {
auto [s, b, d] = q.front();
q.pop_front();
si = s / n, sj = s % n;
bi = b / n, bj = b % n;
if (grid[bi][bj] == 'T') {
return d;
}
for (int k = 0; k < 4; ++k) {
int sx = si + dirs[k], sy = sj + dirs[k + 1];
if (!check(sx, sy)) {
continue;
}
if (sx == bi && sy == bj) {
int bx = bi + dirs[k], by = bj + dirs[k + 1];
if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
continue;
}
vis[f(sx, sy)][f(bx, by)] = true;
q.emplace_back(f(sx, sy), f(bx, by), d + 1);
} else if (!vis[f(sx, sy)][f(bi, bj)]) {
vis[f(sx, sy)][f(bi, bj)] = true;
q.emplace_front(f(sx, sy), f(bi, bj), d);
}
}
}
return -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53 | func minPushBox(grid [][]byte) int {
m, n := len(grid), len(grid[0])
var si, sj, bi, bj int
for i, row := range grid {
for j, c := range row {
if c == 'S' {
si, sj = i, j
} else if c == 'B' {
bi, bj = i, j
}
}
}
f := func(i, j int) int {
return i*n + j
}
check := func(i, j int) bool {
return i >= 0 && i < m && j >= 0 && j < n && grid[i][j] != '#'
}
q := [][]int{[]int{f(si, sj), f(bi, bj), 0}}
vis := make([][]bool, m*n)
for i := range vis {
vis[i] = make([]bool, m*n)
}
vis[f(si, sj)][f(bi, bj)] = true
dirs := [5]int{-1, 0, 1, 0, -1}
for len(q) > 0 {
p := q[0]
q = q[1:]
si, sj, bi, bj = p[0]/n, p[0]%n, p[1]/n, p[1]%n
d := p[2]
if grid[bi][bj] == 'T' {
return d
}
for k := 0; k < 4; k++ {
sx, sy := si+dirs[k], sj+dirs[k+1]
if !check(sx, sy) {
continue
}
if sx == bi && sy == bj {
bx, by := bi+dirs[k], bj+dirs[k+1]
if !check(bx, by) || vis[f(sx, sy)][f(bx, by)] {
continue
}
vis[f(sx, sy)][f(bx, by)] = true
q = append(q, []int{f(sx, sy), f(bx, by), d + 1})
} else if !vis[f(sx, sy)][f(bi, bj)] {
vis[f(sx, sy)][f(bi, bj)] = true
q = append([][]int{[]int{f(sx, sy), f(bi, bj), d}}, q...)
}
}
}
return -1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218 | function minPushBox(grid: string[][]): number {
const [m, n] = [grid.length, grid[0].length];
let [si, sj, bi, bj] = [0, 0, 0, 0];
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (grid[i][j] === 'S') {
[si, sj] = [i, j];
} else if (grid[i][j] === 'B') {
[bi, bj] = [i, j];
}
}
}
const f = (i: number, j: number): number => i * n + j;
const check = (i: number, j: number): boolean =>
i >= 0 && i < m && j >= 0 && j < n && grid[i][j] !== '#';
const q: Deque<[number, number, number]> = new Deque();
const vis: boolean[][] = new Array(m * n).fill(0).map(() => new Array(m * n).fill(false));
q.push([f(si, sj), f(bi, bj), 0]);
vis[f(si, sj)][f(bi, bj)] = true;
const dirs: number[] = [-1, 0, 1, 0, -1];
while (q.size() > 0) {
const [s, b, d] = q.shift()!;
const [si, sj] = [Math.floor(s / n), s % n];
const [bi, bj] = [Math.floor(b / n), b % n];
if (grid[bi][bj] === 'T') {
return d;
}
for (let k = 0; k < 4; ++k) {
const [sx, sy] = [si + dirs[k], sj + dirs[k + 1]];
if (!check(sx, sy)) {
continue;
}
if (sx === bi && sy === bj) {
const [bx, by] = [bi + dirs[k], bj + dirs[k + 1]];
if (!check(bx, by) || vis[f(sx, sy)][f(bx, by)]) {
continue;
}
vis[f(sx, sy)][f(bx, by)] = true;
q.push([f(sx, sy), f(bx, by), d + 1]);
} else if (!vis[f(sx, sy)][f(bi, bj)]) {
vis[f(sx, sy)][f(bi, bj)] = true;
q.unshift([f(sx, sy), f(bi, bj), d]);
}
}
}
return -1;
}
/* 以下是双向列队模板类 */
class CircularDeque<T> {
prev: CircularDeque<T> | null;
next: CircularDeque<T> | null;
begin: number;
end: number;
empty: boolean;
data: T[];
constructor(N: number) {
this.prev = this.next = null;
this.begin = this.end = 0;
this.empty = true;
this.data = Array(N);
}
isFull(): boolean {
return this.end === this.begin && !this.empty;
}
isEmpty(): boolean {
return this.empty;
}
push(val: T): boolean {
if (this.isFull()) return false;
this.empty = false;
this.data[this.end] = val;
this.end = (this.end + 1) % this.data.length;
return true;
}
front(): T | undefined {
return this.isEmpty() ? undefined : this.data[this.begin];
}
back(): T | undefined {
return this.isEmpty() ? undefined : this.data[this.end - 1];
}
pop(): T | undefined {
if (this.isEmpty()) return undefined;
const value = this.data[this.end - 1];
this.end = (this.end - 1) % this.data.length;
if (this.end < 0) this.end += this.data.length;
if (this.end === this.begin) this.empty = true;
return value;
}
unshift(val: T): boolean {
if (this.isFull()) return false;
this.empty = false;
this.begin = (this.begin - 1) % this.data.length;
if (this.begin < 0) this.begin += this.data.length;
this.data[this.begin] = val;
return true;
}
shift(): T | undefined {
if (this.isEmpty()) return undefined;
const value = this.data[this.begin];
this.begin = (this.begin + 1) % this.data.length;
if (this.end === this.begin) this.empty = true;
return value;
}
*values(): Generator<T, void, undefined> {
if (this.isEmpty()) return undefined;
let i = this.begin;
do {
yield this.data[i];
i = (i + 1) % this.data.length;
} while (i !== this.end);
}
}
class Deque<T> {
head: CircularDeque<T>;
tail: CircularDeque<T>;
_size: number;
constructor(collection: T[] = []) {
this.head = new CircularDeque<T>(128);
this.tail = new CircularDeque<T>(128);
this.tail.empty = this.head.empty = false;
this.tail.prev = this.head;
this.head.next = this.tail;
this._size = 0;
for (const item of collection) this.push(item);
}
size(): number {
return this._size;
}
push(val: T): void {
let last = this.tail.prev!;
if (last.isFull()) {
const inserted = new CircularDeque<T>(128);
this.tail.prev = inserted;
inserted.next = this.tail;
last.next = inserted;
inserted.prev = last;
last = inserted;
}
last.push(val);
this._size++;
}
back(): T | undefined {
if (this._size === 0) return;
return this.tail.prev!.back();
}
pop(): T | undefined {
if (this.head.next === this.tail) return undefined;
const last = this.tail.prev!;
const value = last.pop();
if (last.isEmpty()) {
this.tail.prev = last.prev;
last.prev!.next = this.tail;
}
this._size--;
return value;
}
unshift(val: T): void {
let first = this.head.next!;
if (first.isFull()) {
const inserted = new CircularDeque<T>(128);
this.head.next = inserted;
inserted.prev = this.head;
inserted.next = first;
first.prev = inserted;
first = inserted;
}
first.unshift(val);
this._size++;
}
shift(): T | undefined {
if (this.head.next === this.tail) return undefined;
const first = this.head.next!;
const value = first.shift();
if (first.isEmpty()) {
this.head.next = first.next;
first.next!.prev = this.head;
}
this._size--;
return value;
}
front(): T | undefined {
if (this._size === 0) return undefined;
return this.head.next!.front();
}
*values(): Generator<T, void, undefined> {
let node = this.head.next!;
while (node !== this.tail) {
for (const value of node.values()) yield value;
node = node.next!;
}
}
}
|



