1259. 不相交的握手 🔒

题目描述

偶数个人站成一个圆，总人数为 num_people 。每个人与除自己外的一个人握手，所以总共会有 num_people / 2 次握手。

将握手的人之间连线，请你返回连线不会相交的握手方案数。

由于结果可能会很大，请你返回答案模 10^9+7 后的结果。

示例 1：

输入：num_people = 2
输出：1

示例 2：

输入：num_people = 4
输出：2
解释：总共有两种方案，第一种方案是 [(1,2),(3,4)] ，第二种方案是 [(2,3),(4,1)] 。

示例 3：

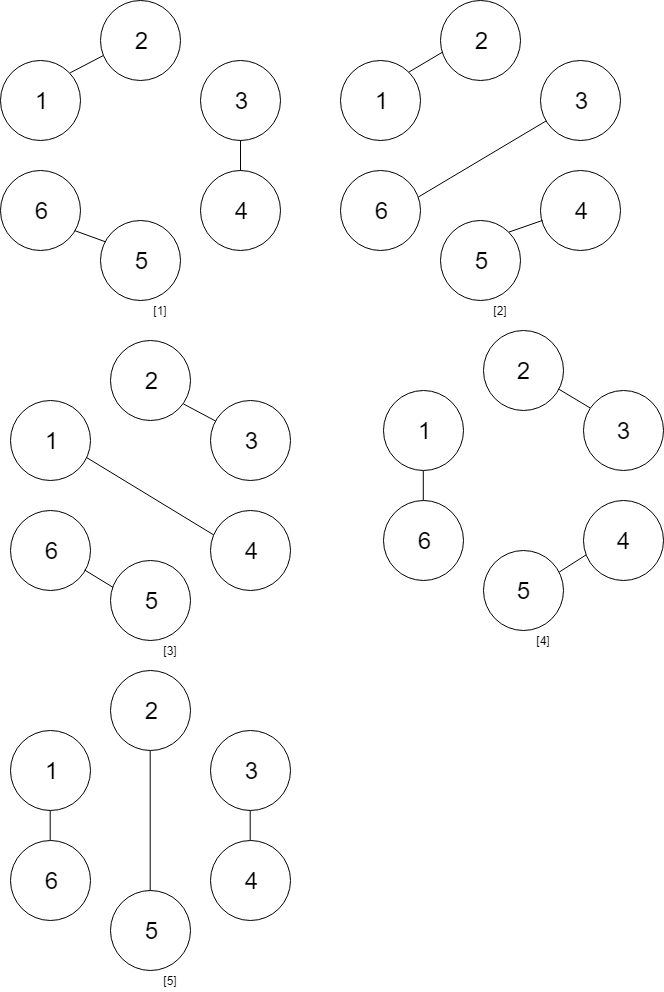
输入：num_people = 6
输出：5

示例 4：

输入：num_people = 8
输出：14

提示：

2 <= num_people <= 1000
num_people % 2 == 0

解法

方法一：记忆化搜索

我们设计一个函数 $dfs(i)$，表示 $i$ 个人的握手方案数。答案为 $dfs(n)$。

函数 $dfs(i)$ 的执行逻辑如下：

如果 $i \lt 2$，那么只有一种握手方案，即不握手，返回 $1$。
否则，我们可以枚举第一个人与谁握手，记剩余的左边的人数为 $l$，右边的人数为 $r=i-l-2$，那么有 $dfs(i)= \sum_{l=0}^{i-1} dfs(l) \times dfs(r)$。

为了避免重复计算，我们使用记忆化搜索的方法。

时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。其中 $n$ 为 $numPeople$ 的大小。

Python3JavaC++GoTypeScript

class Solution:
    def numberOfWays(self, numPeople: int) -> int:
        @cache
        def dfs(i: int) -> int:
            if i < 2:
                return 1
            ans = 0
            for l in range(0, i, 2):
                r = i - l - 2
                ans += dfs(l) * dfs(r)
                ans %= mod
            return ans

        mod = 10**9 + 7
        return dfs(numPeople)

class Solution {
    private int[] f;
    private final int mod = (int) 1e9 + 7;

    public int numberOfWays(int numPeople) {
        f = new int[numPeople + 1];
        return dfs(numPeople);
    }

    private int dfs(int i) {
        if (i < 2) {
            return 1;
        }
        if (f[i] != 0) {
            return f[i];
        }
        for (int l = 0; l < i; l += 2) {
            int r = i - l - 2;
            f[i] = (int) ((f[i] + (1L * dfs(l) * dfs(r) % mod)) % mod);
        }
        return f[i];
    }
}

class Solution {
public:
    int numberOfWays(int numPeople) {
        const int mod = 1e9 + 7;
        int f[numPeople + 1];
        memset(f, 0, sizeof(f));
        function<int(int)> dfs = [&](int i) {
            if (i < 2) {
                return 1;
            }
            if (f[i]) {
                return f[i];
            }
            for (int l = 0; l < i; l += 2) {
                int r = i - l - 2;
                f[i] = (f[i] + 1LL * dfs(l) * dfs(r) % mod) % mod;
            }
            return f[i];
        };
        return dfs(numPeople);
    }
};

func numberOfWays(numPeople int) int {
    const mod int = 1e9 + 7
    f := make([]int, numPeople+1)
    var dfs func(int) int
    dfs = func(i int) int {
        if i < 2 {
            return 1
        }
        if f[i] != 0 {
            return f[i]
        }
        for l := 0; l < i; l += 2 {
            r := i - l - 2
            f[i] = (f[i] + dfs(l)*dfs(r)) % mod
        }
        return f[i]
    }
    return dfs(numPeople)
}

function numberOfWays(numPeople: number): number {
    const mod = 10 ** 9 + 7;
    const f: number[] = Array(numPeople + 1).fill(0);
    const dfs = (i: number): number => {
        if (i < 2) {
            return 1;
        }
        if (f[i] !== 0) {
            return f[i];
        }
        for (let l = 0; l < i; l += 2) {
            const r = i - l - 2;
            f[i] += Number((BigInt(dfs(l)) * BigInt(dfs(r))) % BigInt(mod));
            f[i] %= mod;
        }
        return f[i];
    };
    return dfs(numPeople);
}

1259. 不相交的握手 🔒

题目描述

解法

方法一：记忆化搜索

评论