


题目描述
在一个 下标从 0 开始 的 8 x 8 棋盘上,可能有多个黑皇后和一个白国王。
给你一个二维整数数组 queens,其中 queens[i] = [xQueeni, yQueeni] 表示第 i 个黑皇后在棋盘上的位置。还给你一个长度为 2 的整数数组 king,其中 king = [xKing, yKing] 表示白国王的位置。
返回 能够直接攻击国王的黑皇后的坐标。你可以以 任何顺序 返回答案。
示例 1:

输入:queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出:[[0,1],[1,0],[3,3]]
解释:上面的图示显示了三个可以直接攻击国王的皇后和三个不能攻击国王的皇后(用红色虚线标记)。
示例 2:
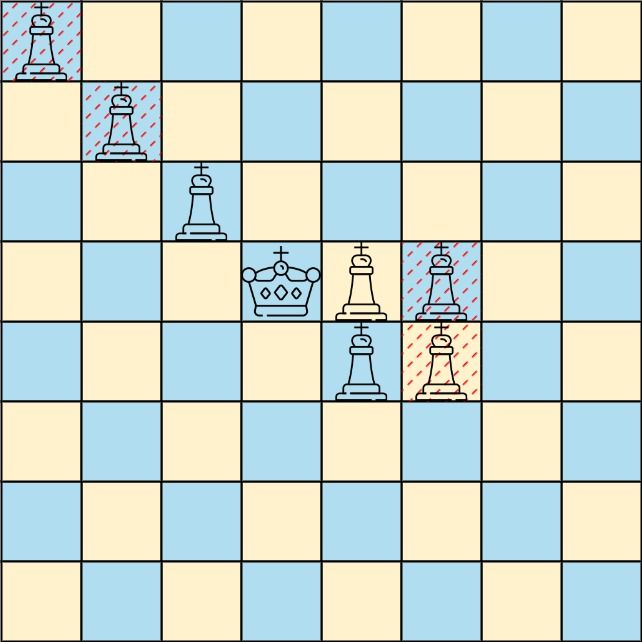
输入:queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出:[[2,2],[3,4],[4,4]]
解释:上面的图示显示了三个能够直接攻击国王的黑皇后和三个不能攻击国王的黑皇后(用红色虚线标记)。
提示:
1 <= queens.length < 64queens[i].length == king.length == 20 <= xQueeni, yQueeni, xKing, yKing < 8- 所有给定的位置都是 唯一 的。
解法
方法一:直接搜索
我们先将所有皇后的位置存入哈希表或者二维数组 \(s\) 中。
接下来,我们从国王的位置开始,依次向上、下、左、右、左上、右上、左下、右下八个方向搜索,如果某个方向上存在皇后,那么就将其位置加入答案中,并且停止继续搜索该方向。
搜索结束后,返回答案即可。
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n^2)\)。本题中 \(n = 8\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution:
def queensAttacktheKing(
self, queens: List[List[int]], king: List[int]
) -> List[List[int]]:
n = 8
s = {(i, j) for i, j in queens}
ans = []
for a in range(-1, 2):
for b in range(-1, 2):
if a or b:
x, y = king
while 0 <= x + a < n and 0 <= y + b < n:
x, y = x + a, y + b
if (x, y) in s:
ans.append([x, y])
break
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
final int n = 8;
var s = new boolean[n][n];
for (var q : queens) {
s[q[0]][q[1]] = true;
}
List<List<Integer>> ans = new ArrayList<>();
for (int a = -1; a <= 1; ++a) {
for (int b = -1; b <= 1; ++b) {
if (a != 0 || b != 0) {
int x = king[0] + a, y = king[1] + b;
while (x >= 0 && x < n && y >= 0 && y < n) {
if (s[x][y]) {
ans.add(List.of(x, y));
break;
}
x += a;
y += b;
}
}
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
public:
vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
int n = 8;
bool s[8][8]{};
for (auto& q : queens) {
s[q[0]][q[1]] = true;
}
vector<vector<int>> ans;
for (int a = -1; a <= 1; ++a) {
for (int b = -1; b <= 1; ++b) {
if (a || b) {
int x = king[0] + a, y = king[1] + b;
while (x >= 0 && x < n && y >= 0 && y < n) {
if (s[x][y]) {
ans.push_back({x, y});
break;
}
x += a;
y += b;
}
}
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func queensAttacktheKing(queens [][]int, king []int) (ans [][]int) {
n := 8
s := [8][8]bool{}
for _, q := range queens {
s[q[0]][q[1]] = true
}
for a := -1; a <= 1; a++ {
for b := -1; b <= 1; b++ {
if a != 0 || b != 0 {
x, y := king[0]+a, king[1]+b
for 0 <= x && x < n && 0 <= y && y < n {
if s[x][y] {
ans = append(ans, []int{x, y})
break
}
x += a
y += b
}
}
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | function queensAttacktheKing(queens: number[][], king: number[]): number[][] {
const n = 8;
const s: boolean[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => false));
queens.forEach(([x, y]) => (s[x][y] = true));
const ans: number[][] = [];
for (let a = -1; a <= 1; ++a) {
for (let b = -1; b <= 1; ++b) {
if (a || b) {
let [x, y] = [king[0] + a, king[1] + b];
while (x >= 0 && x < n && y >= 0 && y < n) {
if (s[x][y]) {
ans.push([x, y]);
break;
}
x += a;
y += b;
}
}
}
}
return ans;
}
|




