1111. 有效括号的嵌套深度

题目描述

有效括号字符串 定义：对于每个左括号，都能找到与之对应的右括号，反之亦然。详情参见题末「有效括号字符串」部分。

嵌套深度 depth 定义：即有效括号字符串嵌套的层数，depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。

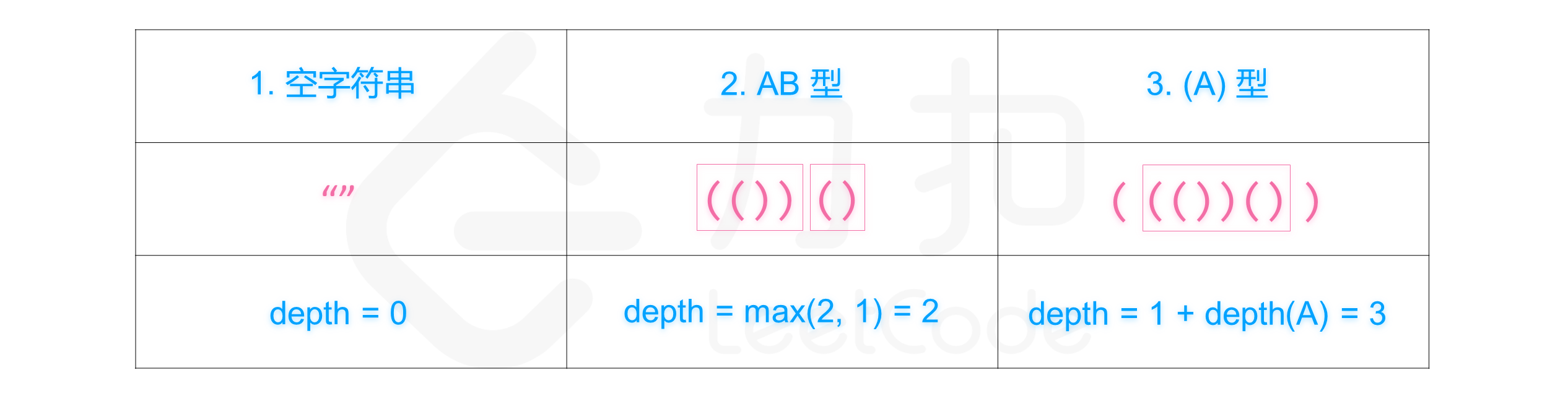
有效括号字符串类型与对应的嵌套深度计算方法如下图所示：

给你一个「有效括号字符串」 seq，请你将其分成两个不相交的有效括号字符串，A 和 B，并使这两个字符串的深度最小。

不相交：每个 seq[i] 只能分给 A 和 B 二者中的一个，不能既属于 A 也属于 B 。
A 或 B 中的元素在原字符串中可以不连续。
A.length + B.length = seq.length
深度最小：max(depth(A), depth(B)) 的可能取值最小。

划分方案用一个长度为 seq.length 的答案数组 answer 表示，编码规则如下：

answer[i] = 0，seq[i] 分给 A 。
answer[i] = 1，seq[i] 分给 B 。

如果存在多个满足要求的答案，只需返回其中任意一个即可。

示例 1：

输入：seq = "(()())"
输出：[0,1,1,1,1,0]

示例 2：

输入：seq = "()(())()"
输出：[0,0,0,1,1,0,1,1]
解释：本示例答案不唯一。
按此输出 A = "()()", B = "()()", max(depth(A), depth(B)) = 1，它们的深度最小。
像 [1,1,1,0,0,1,1,1]，也是正确结果，其中 A = "()()()", B = "()", max(depth(A), depth(B)) = 1 。

提示：

1 < seq.size <= 10000

有效括号字符串：

仅由 "(" 和 ")" 构成的字符串，对于每个左括号，都能找到与之对应的右括号，反之亦然。
下述几种情况同样属于有效括号字符串：

  1. 空字符串
  2. 连接，可以记作 AB（A 与 B 连接），其中 A 和 B 都是有效括号字符串
  3. 嵌套，可以记作 (A)，其中 A 是有效括号字符串

嵌套深度：

类似地，我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S)：

  1. s 为空时，depth("") = 0
  2. s 为 A 与 B 连接时，depth(A + B) = max(depth(A), depth(B))，其中 A 和 B 都是有效括号字符串
  3. s 为嵌套情况，depth("(" + A + ")") = 1 + depth(A)，其中 A 是有效括号字符串

例如：""，"()()"，和 "()(()())" 都是有效括号字符串，嵌套深度分别为 0，1，2，而 ")(" 和 "(()" 都不是有效括号字符串。

解法

方法一：贪心

我们用一个变量 $x$ 维护当前括号的平衡度，也就是左括号的数量减去右括号的数量。

遍历字符串 $seq$，更新 $x$ 的值。如果 $x$ 为奇数，我们将当前的左括号分给 $A$，否则分给 $B$。

时间复杂度 $O(n)$，其中 $n$ 是字符串 $seq$ 的长度。忽略答案数组的空间消耗，空间复杂度 $O(1)$。

Python3JavaC++GoTypeScript

class Solution:
    def maxDepthAfterSplit(self, seq: str) -> List[int]:
        ans = [0] * len(seq)
        x = 0
        for i, c in enumerate(seq):
            if c == "(":
                ans[i] = x & 1
                x += 1
            else:
                x -= 1
                ans[i] = x & 1
        return ans

class Solution {
    public int[] maxDepthAfterSplit(String seq) {
        int n = seq.length();
        int[] ans = new int[n];
        for (int i = 0, x = 0; i < n; ++i) {
            if (seq.charAt(i) == '(') {
                ans[i] = x++ & 1;
            } else {
                ans[i] = --x & 1;
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> maxDepthAfterSplit(string seq) {
        int n = seq.size();
        vector<int> ans(n);
        for (int i = 0, x = 0; i < n; ++i) {
            if (seq[i] == '(') {
                ans[i] = x++ & 1;
            } else {
                ans[i] = --x & 1;
            }
        }
        return ans;
    }
};

func maxDepthAfterSplit(seq string) []int {
    n := len(seq)
    ans := make([]int, n)
    for i, x := 0, 0; i < n; i++ {
        if seq[i] == '(' {
            ans[i] = x & 1
            x++
        } else {
            x--
            ans[i] = x & 1
        }
    }
    return ans
}

function maxDepthAfterSplit(seq: string): number[] {
    const n = seq.length;
    const ans: number[] = new Array(n);
    for (let i = 0, x = 0; i < n; ++i) {
        if (seq[i] === '(') {
            ans[i] = x++ & 1;
        } else {
            ans[i] = --x & 1;
        }
    }
    return ans;
}

1111. 有效括号的嵌套深度

题目描述

解法

方法一：贪心

评论