


题目描述
你有一个凸的 n 边形,其每个顶点都有一个整数值。给定一个整数数组 values ,其中 values[i] 是第 i 个顶点的值(即 顺时针顺序 )。
假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。
返回 多边形进行三角剖分后可以得到的最低分 。
示例 1:
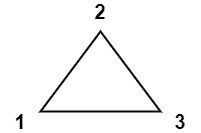
输入:values = [1,2,3]
输出:6
解释:多边形已经三角化,唯一三角形的分数为 6。
示例 2:
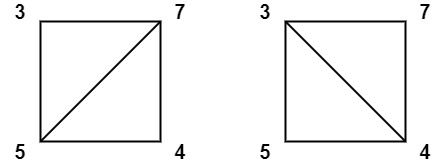
输入:values = [3,7,4,5]
输出:144
解释:有两种三角剖分,可能得分分别为:3*7*5 + 4*5*7 = 245,或 3*4*5 + 3*4*7 = 144。最低分数为 144。
示例 3:
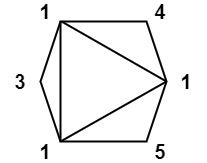
输入:values = [1,3,1,4,1,5]
输出:13
解释:最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。
提示:
n == values.length3 <= n <= 501 <= values[i] <= 100
解法
方法一:记忆化搜索
我们设计一个函数 \(dfs(i, j)\),表示将多边形的顶点 \(i\) 到 \(j\) 进行三角剖分后的最低分数。那么答案就是 \(dfs(0, n - 1)\)。
函数 \(dfs(i, j)\) 的计算过程如下:
如果 \(i + 1 = j\),说明多边形只有两个顶点,无法进行三角剖分,返回 \(0\);
否则,我们枚举 \(i\) 和 \(j\) 之间的一个顶点 \(k\),即 \(i \lt k \lt j\),将多边形的顶点 \(i\) 到 \(j\) 进行三角剖分,可以分为两个子问题:将多边形的顶点 \(i\) 到 \(k\) 进行三角剖分,以及将多边形的顶点 \(k\) 到 \(j\) 进行三角剖分。这两个子问题的最低分数分别为 \(dfs(i, k)\) 和 \(dfs(k, j)\),而顶点 \(i\), \(j\) 和 \(k\) 构成的三角形的分数为 \(values[i] \times values[k] \times values[j]\)。那么,此次三角剖分的最低分数为 \(dfs(i, k) + dfs(k, j) + values[i] \times values[k] \times values[j]\),我们取所有可能的最小值,即为 \(dfs(i, j)\) 的值。
为了避免重复计算,我们可以使用记忆化搜索,即使用哈希表或者数组来存储已经计算过的函数值。
最后,我们返回 \(dfs(0, n - 1)\) 即可。
时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\)。其中 \(n\) 为多边形的顶点数。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
@cache
def dfs(i: int, j: int) -> int:
if i + 1 == j:
return 0
return min(
dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return dfs(0, len(values) - 1)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | class Solution {
private int n;
private int[] values;
private Integer[][] f;
public int minScoreTriangulation(int[] values) {
n = values.length;
this.values = values;
f = new Integer[n][n];
return dfs(0, n - 1);
}
private int dfs(int i, int j) {
if (i + 1 == j) {
return 0;
}
if (f[i][j] != null) {
return f[i][j];
}
int ans = 1 << 30;
for (int k = i + 1; k < j; ++k) {
ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
return f[i][j] = ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
function<int(int, int)> dfs = [&](int i, int j) -> int {
if (i + 1 == j) {
return 0;
}
if (f[i][j]) {
return f[i][j];
}
int ans = 1 << 30;
for (int k = i + 1; k < j; ++k) {
ans = min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
return f[i][j] = ans;
};
return dfs(0, n - 1);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
var dfs func(int, int) int
dfs = func(i, j int) int {
if i+1 == j {
return 0
}
if f[i][j] != 0 {
return f[i][j]
}
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], dfs(i, k)+dfs(k, j)+values[i]*values[k]*values[j])
}
return f[i][j]
}
return dfs(0, n-1)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
const dfs = (i: number, j: number): number => {
if (i + 1 === j) {
return 0;
}
if (f[i][j] > 0) {
return f[i][j];
}
let ans = 1 << 30;
for (let k = i + 1; k < j; ++k) {
ans = Math.min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
}
f[i][j] = ans;
return ans;
};
return dfs(0, n - 1);
}
|
方法二:动态规划
我们可以将方法一中的记忆化搜索改为动态规划。
定义 \(f[i][j]\) 表示将多边形的顶点 \(i\) 到 \(j\) 进行三角剖分后的最低分数。初始时 \(f[i][j]=0\),答案为 \(f[0][n-1]\)。
对于 \(f[i][j]\)(这里要求 \(i + 1 \lt j\)),我们先将 \(f[i][j]\) 初始化为 \(\infty\)。
我们枚举 \(i\) 和 \(j\) 之间的一个顶点 \(k\),即 \(i \lt k \lt j\),将多边形的顶点 \(i\) 到 \(j\) 进行三角剖分,可以分为两个子问题:将多边形的顶点 \(i\) 到 \(k\) 进行三角剖分,以及将多边形的顶点 \(k\) 到 \(j\) 进行三角剖分。这两个子问题的最低分数分别为 \(f[i][k]\) 和 \(f[k][j]\),而顶点 \(i\), \(j\) 和 \(k\) 构成的三角形的分数为 \(values[i] \times values[k] \times values[j]\)。那么,此次三角剖分的最低分数为 \(f[i][k] + f[k][j] + values[i] \times values[k] \times values[j]\),我们取所有可能的最小值,即为 \(f[i][j]\) 的值。
综上,我们可以得到状态转移方程:
\[
f[i][j]=
\begin{cases}
0, & i+1=j \\
\min_{i<k<j} \{f[i][k]+f[k][j]+values[i] \times values[k] \times values[j]\}, & i+1<j
\end{cases}
\]
注意,在枚举 \(i\) 和 \(j\) 时,我们可以有两种枚举方式:
- 从大到小枚举 \(i\),从小到大枚举 \(j\),这样可以保证在计算状态 \(f[i][j]\) 时,状态 \(f[i][k]\) 和 \(f[k][j]\) 都已经计算过了;
- 从小到大枚举区间长度 \(l\),其中 \(3 \leq l \leq n\),然后枚举区间左端点 \(i\),那么可以得到右端点 \(j=i + l - 1\),这样也可以保证在计算较大区间 \(f[i][j]\) 时,较小区间 \(f[i][k]\) 和 \(f[k][j]\) 都已经计算过了。
最后,我们返回 \(f[0][n-1]\) 即可。
时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\)。其中 \(n\) 为多边形的顶点数。
相似题目:
| class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
n = len(values)
f = [[0] * n for _ in range(n)]
for i in range(n - 3, -1, -1):
for j in range(i + 2, n):
f[i][j] = min(
f[i][k] + f[k][j] + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return f[0][-1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution {
public int minScoreTriangulation(int[] values) {
int n = values.length;
int[][] f = new int[n][n];
for (int i = n - 3; i >= 0; --i) {
for (int j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j]
= Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
for (int i = n - 3; i >= 0; --i) {
for (int j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13 | func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
for i := n - 3; i >= 0; i-- {
for j := i + 2; j < n; j++ {
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
}
}
}
return f[0][n-1]
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13 | function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
for (let i = n - 3; i >= 0; --i) {
for (let j = i + 2; j < n; ++j) {
f[i][j] = 1 << 30;
for (let k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
|
方法三
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
n = len(values)
f = [[0] * n for _ in range(n)]
for l in range(3, n + 1):
for i in range(n - l + 1):
j = i + l - 1
f[i][j] = min(
f[i][k] + f[k][j] + values[i] * values[k] * values[j]
for k in range(i + 1, j)
)
return f[0][-1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public int minScoreTriangulation(int[] values) {
int n = values.length;
int[][] f = new int[n][n];
for (int l = 3; l <= n; ++l) {
for (int i = 0; i + l - 1 < n; ++i) {
int j = i + l - 1;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j]
= Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof(f));
for (int l = 3; l <= n; ++l) {
for (int i = 0; i + l - 1 < n; ++i) {
int j = i + l - 1;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | func minScoreTriangulation(values []int) int {
n := len(values)
f := [50][50]int{}
for l := 3; l <= n; l++ {
for i := 0; i+l-1 < n; i++ {
j := i + l - 1
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+values[i]*values[k]*values[j])
}
}
}
return f[0][n-1]
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | function minScoreTriangulation(values: number[]): number {
const n = values.length;
const f: number[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => 0));
for (let l = 3; l <= n; ++l) {
for (let i = 0; i + l - 1 < n; ++i) {
const j = i + l - 1;
f[i][j] = 1 << 30;
for (let k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + values[i] * values[k] * values[j]);
}
}
}
return f[0][n - 1];
}
|





