二叉树
广度优先搜索
树
题目描述
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
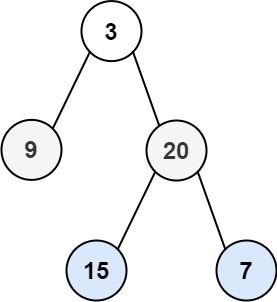
输入: root = [3,9,20,null,null,15,7]
输出: [[3],[9,20],[15,7]]
示例 2:
输入: root = [1]
输出: [[1]]
示例 3:
输入: root = []
输出: []
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
解法
方法一:BFS
我们可以使用 BFS 的方法来解决这道题。首先将根节点入队,然后不断地进行以下操作,直到队列为空:
遍历当前队列中的所有节点,将它们的值存储到一个临时数组 \(t\) 中,然后将它们的孩子节点入队。
将临时数组 \(t\) 存储到答案数组中。
最后返回答案数组即可。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是二叉树的节点个数。
Python3 Java C++ Go TypeScript Rust JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def levelOrder ( self , root : Optional [ TreeNode ]) -> List [ List [ int ]]:
ans = []
if root is None :
return ans
q = deque ([ root ])
while q :
t = []
for _ in range ( len ( q )):
node = q . popleft ()
t . append ( node . val )
if node . left :
q . append ( node . left )
if node . right :
q . append ( node . right )
ans . append ( t )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List < List < Integer >> levelOrder ( TreeNode root ) {
List < List < Integer >> ans = new ArrayList <> ();
if ( root == null ) {
return ans ;
}
Deque < TreeNode > q = new ArrayDeque <> ();
q . offer ( root );
while ( ! q . isEmpty ()) {
List < Integer > t = new ArrayList <> ();
for ( int n = q . size (); n > 0 ; -- n ) {
TreeNode node = q . poll ();
t . add ( node . val );
if ( node . left != null ) {
q . offer ( node . left );
}
if ( node . right != null ) {
q . offer ( node . right );
}
}
ans . add ( t );
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
vector < vector < int >> levelOrder ( TreeNode * root ) {
vector < vector < int >> ans ;
if ( ! root ) return ans ;
queue < TreeNode *> q {{ root }};
while ( ! q . empty ()) {
vector < int > t ;
for ( int n = q . size (); n ; -- n ) {
auto node = q . front ();
q . pop ();
t . push_back ( node -> val );
if ( node -> left ) {
q . push ( node -> left );
}
if ( node -> right ) {
q . push ( node -> right );
}
}
ans . push_back ( t );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder ( root * TreeNode ) ( ans [][] int ) {
if root == nil {
return
}
q := [] * TreeNode { root }
for len ( q ) > 0 {
t := [] int {}
for n := len ( q ); n > 0 ; n -- {
node := q [ 0 ]
q = q [ 1 :]
t = append ( t , node . Val )
if node . Left != nil {
q = append ( q , node . Left )
}
if node . Right != nil {
q = append ( q , node . Right )
}
}
ans = append ( ans , t )
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function levelOrder ( root : TreeNode | null ) : number [][] {
const ans : number [][] = [];
if ( ! root ) {
return ans ;
}
const q : TreeNode [] = [ root ];
while ( q . length ) {
const t : number [] = [];
const qq : TreeNode [] = [];
for ( const { val , left , right } of q ) {
t . push ( val );
left && qq . push ( left );
right && qq . push ( right );
}
ans . push ( t );
q . splice ( 0 , q . length , ... qq );
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: cell :: RefCell ;
use std :: collections :: VecDeque ;
use std :: rc :: Rc ;
impl Solution {
pub fn level_order ( root : Option < Rc < RefCell < TreeNode >>> ) -> Vec < Vec < i32 >> {
let mut ans = Vec :: new ();
if let Some ( root_node ) = root {
let mut q = VecDeque :: new ();
q . push_back ( root_node );
while ! q . is_empty () {
let mut t = Vec :: new ();
for _ in 0 .. q . len () {
if let Some ( node ) = q . pop_front () {
let node_ref = node . borrow ();
t . push ( node_ref . val );
if let Some ( ref left ) = node_ref . left {
q . push_back ( Rc :: clone ( left ));
}
if let Some ( ref right ) = node_ref . right {
q . push_back ( Rc :: clone ( right ));
}
}
}
ans . push ( t );
}
}
ans
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function ( root ) {
const ans = [];
if ( ! root ) {
return ans ;
}
const q = [ root ];
while ( q . length ) {
const t = [];
const qq = [];
for ( const { val , left , right } of q ) {
t . push ( val );
left && qq . push ( left );
right && qq . push ( right );
}
ans . push ( t );
q . splice ( 0 , q . length , ... qq );
}
return ans ;
};
GitHub