跳转至

1001. 网格照明

题目描述

在大小为 n x n 的网格 grid 上，每个单元格都有一盏灯，最初灯都处于 关闭 状态。

给你一个由灯的位置组成的二维数组 lamps ，其中 lamps[i] = [rowi, coli] 表示 打开 位于 grid[rowi][coli] 的灯。即便同一盏灯可能在 lamps 中多次列出，不会影响这盏灯处于 打开 状态。

当一盏灯处于打开状态，它将会照亮 自身所在单元格 以及同一 行 、同一 列 和两条 对角线 上的 所有其他单元格 。

另给你一个二维数组 queries ，其中 queries[j] = [rowj, colj] 。对于第 j 个查询，如果单元格 [rowj, colj] 是被照亮的，则查询结果为 1 ，否则为 0 。在第 j 次查询之后 [按照查询的顺序] ，关闭 位于单元格 grid[rowj][colj] 上及相邻 8 个方向上（与单元格 grid[rowi][coli] 共享角或边）的任何灯。

返回一个整数数组 ans 作为答案， ans[j] 应等于第 j 次查询 queries[j] 的结果，1 表示照亮，0 表示未照亮。

 

示例 1：

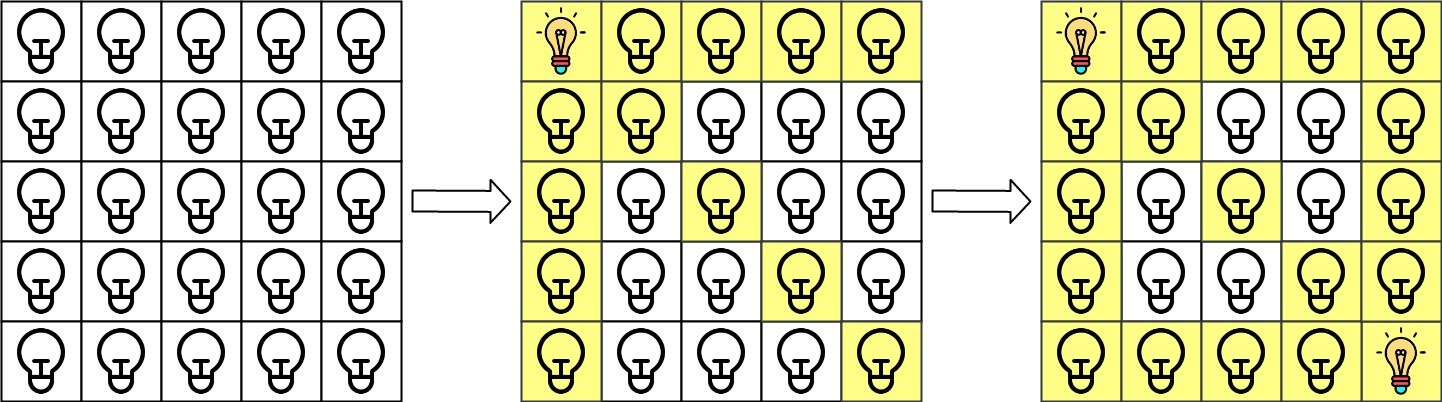
输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出：[1,0]
解释：最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1] 是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。

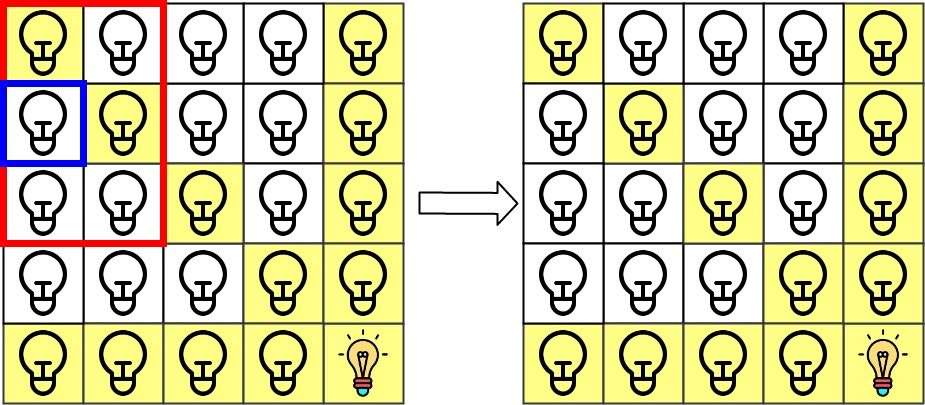
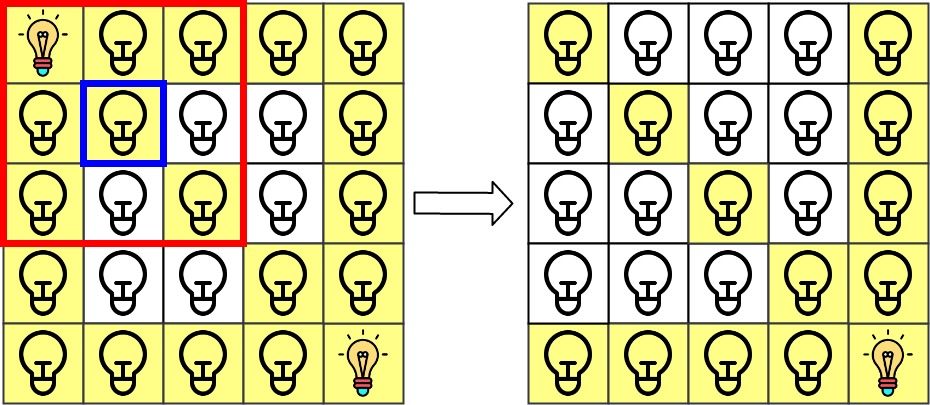第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0 。然后，关闭红色矩形中的所有灯。

示例 2：

输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出：[1,1]

示例 3：

输入：n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出：[1,1,0]

 

提示：

  • 1 <= n <= 109
  • 0 <= lamps.length <= 20000
  • 0 <= queries.length <= 20000
  • lamps[i].length == 2
  • 0 <= rowi, coli < n
  • queries[j].length == 2
  • 0 <= rowj, colj < n

解法

方法一：哈希表

假设一盏灯的坐标为 $(x, y)$，那么它所在的行的数值为 $x$，列的数值为 $y$，正对角线的数值为 $x-y$，反对角线的数值为 $x+y$。确定某一直线的唯一数值标识后，我们就可以通过哈希表来记录某一直线所拥有的灯的数目。

我们遍历数组 $\textit{lamps}$，将当前遍历到的灯所在的行、列和正、反对角线拥有灯的数目分别加 $1$。

注意，在处理 $\textit{lamps}$ 时，需要进行去重，因为我们将重复的灯看作同一盏灯。

接下来，我们遍历 queries，判断当前查询点所在的行，列和正、反对角线是否有灯，如果有，则置 $1$，即该点在查询时是被照亮的。然后进行关闭操作，查找查询点所在的八近邻点及它本身是否有灯，如果有，将该点所在的行、列和正、反对角线的灯数目分别减 $1$，并且将灯从网格中去掉。

最后，返回答案数组即可。

时间复杂度 $O(m + q)$，其中 $m$ 和 $q$ 分别为数组 $\textit{lamps}$ 和 $\textit{queries}$ 的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def gridIllumination(
        self, n: int, lamps: List[List[int]], queries: List[List[int]]
    ) -> List[int]:
        s = {(i, j) for i, j in lamps}
        row, col, diag1, diag2 = Counter(), Counter(), Counter(), Counter()
        for i, j in s:
            row[i] += 1
            col[j] += 1
            diag1[i - j] += 1
            diag2[i + j] += 1
        ans = [0] * len(queries)
        for k, (i, j) in enumerate(queries):
            if row[i] or col[j] or diag1[i - j] or diag2[i + j]:
                ans[k] = 1
            for x in range(i - 1, i + 2):
                for y in range(j - 1, j + 2):
                    if (x, y) in s:
                        s.remove((x, y))
                        row[x] -= 1
                        col[y] -= 1
                        diag1[x - y] -= 1
                        diag2[x + y] -= 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    private int n;
    public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {
        this.n = n;
        Set<Long> s = new HashSet<>();
        Map<Integer, Integer> row = new HashMap<>();
        Map<Integer, Integer> col = new HashMap<>();
        Map<Integer, Integer> diag1 = new HashMap<>();
        Map<Integer, Integer> diag2 = new HashMap<>();
        for (var lamp : lamps) {
            int i = lamp[0], j = lamp[1];
            if (s.add(f(i, j))) {
                merge(row, i, 1);
                merge(col, j, 1);
                merge(diag1, i - j, 1);
                merge(diag2, i + j, 1);
            }
        }
        int m = queries.length;
        int[] ans = new int[m];
        for (int k = 0; k < m; ++k) {
            int i = queries[k][0], j = queries[k][1];
            if (exist(row, i) || exist(col, j) || exist(diag1, i - j) || exist(diag2, i + j)) {
                ans[k] = 1;
            }
            for (int x = i - 1; x <= i + 1; ++x) {
                for (int y = j - 1; y <= j + 1; ++y) {
                    if (x < 0 || x >= n || y < 0 || y >= n || !s.contains(f(x, y))) {
                        continue;
                    }
                    s.remove(f(x, y));
                    merge(row, x, -1);
                    merge(col, y, -1);
                    merge(diag1, x - y, -1);
                    merge(diag2, x + y, -1);
                }
            }
        }
        return ans;
    }

    private void merge(Map<Integer, Integer> cnt, int x, int d) {
        if (cnt.merge(x, d, Integer::sum) == 0) {
            cnt.remove(x);
        }
    }

    private boolean exist(Map<Integer, Integer> cnt, int x) {
        return cnt.getOrDefault(x, 0) > 0;
    }

    private long f(long i, long j) {
        return i * n + j;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    vector<int> gridIllumination(int n, vector<vector<int>>& lamps, vector<vector<int>>& queries) {
        auto f = [&](int i, int j) -> long long {
            return (long long) i * n + j;
        };
        unordered_set<long long> s;
        unordered_map<int, int> row, col, diag1, diag2;
        for (auto& lamp : lamps) {
            int i = lamp[0], j = lamp[1];
            if (!s.count(f(i, j))) {
                s.insert(f(i, j));
                row[i]++;
                col[j]++;
                diag1[i - j]++;
                diag2[i + j]++;
            }
        }
        int m = queries.size();
        vector<int> ans(m);
        for (int k = 0; k < m; ++k) {
            int i = queries[k][0], j = queries[k][1];
            if (row[i] > 0 || col[j] > 0 || diag1[i - j] > 0 || diag2[i + j] > 0) {
                ans[k] = 1;
            }
            for (int x = i - 1; x <= i + 1; ++x) {
                for (int y = j - 1; y <= j + 1; ++y) {
                    if (x < 0 || x >= n || y < 0 || y >= n || !s.count(f(x, y))) {
                        continue;
                    }
                    s.erase(f(x, y));
                    row[x]--;
                    col[y]--;
                    diag1[x - y]--;
                    diag2[x + y]--;
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func gridIllumination(n int, lamps [][]int, queries [][]int) []int {
    row, col, diag1, diag2 := map[int]int{}, map[int]int{}, map[int]int{}, map[int]int{}
    type pair struct{ x, y int }
    s := map[pair]bool{}
    for _, lamp := range lamps {
        i, j := lamp[0], lamp[1]
        p := pair{i, j}
        if !s[p] {
            s[p] = true
            row[i]++
            col[j]++
            diag1[i-j]++
            diag2[i+j]++
        }
    }
    m := len(queries)
    ans := make([]int, m)
    for k, q := range queries {
        i, j := q[0], q[1]
        if row[i] > 0 || col[j] > 0 || diag1[i-j] > 0 || diag2[i+j] > 0 {
            ans[k] = 1
        }
        for x := i - 1; x <= i+1; x++ {
            for y := j - 1; y <= j+1; y++ {
                p := pair{x, y}
                if s[p] {
                    s[p] = false
                    row[x]--
                    col[y]--
                    diag1[x-y]--
                    diag2[x+y]--
                }
            }
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function gridIllumination(n: number, lamps: number[][], queries: number[][]): number[] {
    const row = new Map<number, number>();
    const col = new Map<number, number>();
    const diag1 = new Map<number, number>();
    const diag2 = new Map<number, number>();
    const s = new Set<number>();
    for (const [i, j] of lamps) {
        if (s.has(i * n + j)) {
            continue;
        }
        s.add(i * n + j);
        row.set(i, (row.get(i) || 0) + 1);
        col.set(j, (col.get(j) || 0) + 1);
        diag1.set(i - j, (diag1.get(i - j) || 0) + 1);
        diag2.set(i + j, (diag2.get(i + j) || 0) + 1);
    }
    const ans: number[] = [];
    for (const [i, j] of queries) {
        if (row.get(i)! > 0 || col.get(j)! > 0 || diag1.get(i - j)! > 0 || diag2.get(i + j)! > 0) {
            ans.push(1);
        } else {
            ans.push(0);
        }
        for (let x = i - 1; x <= i + 1; ++x) {
            for (let y = j - 1; y <= j + 1; ++y) {
                if (x < 0 || x >= n || y < 0 || y >= n || !s.has(x * n + y)) {
                    continue;
                }
                s.delete(x * n + y);
                row.set(x, row.get(x)! - 1);
                col.set(y, col.get(y)! - 1);
                diag1.set(x - y, diag1.get(x - y)! - 1);
                diag2.set(x + y, diag2.get(x + y)! - 1);
            }
        }
    }
    return ans;
}

评论